I took another look at Quantum Field Theory for the Gifted Amateur by Lancaster & Blundell, and I have to say, after looking at just the first chapter, I found myself becoming acutely depressed, listening to the freezing cold winds howling outside, knowing full well that I have a difficult enough time just representing 2-dimensional vector addition geometrically. I get it that Schopenhauer had an intuitive understanding of these things, but I seriously doubt that he would go through the required baby-steps necessary for constructing mathematical representations of these mysteries, these hidden properties. [see footnote] Myself, I will most likely die before I am able to appreciate such a book as Quantum Field Theory for the Gifted Amateur by Lancaster, circa 2014.
Having confessed that to myself, I will still leave a suggestion here (to a future self) that there is another option (when you're ready [after going over Classical and Modern Physics texts]) that may be an ever so slightly more gentle approach, mostly because a solution manual is available:
http://quantumfieldtheory.info/Student Friendly Quantum Field Theory [Klauber]___________________________________________________________________________
AN IMPORTANT MESSAGE FROM the author of the Student Friendly QFT text, Robert Klauber:
Electronic CopiesI have become aware that someone has scanned my book and pdf copies are being passed around, in violation of copyright laws.
It has been a pleasure for me to give you, the end user, an intro to QFT that most believe is far easier to understand than, and saves a whole lot of time over, other texts on the market. I thought only of you during the years spent writing the book, and from looking around this website, you can see I am still doing so.
So, in return, I ask you to help me. If you are using, or thinking of using, a pirated electronic copy of the book, then please purchase a physical copy.
The soft cover version can be had for $57, which is less than half the cost per word of any other text covering the same material. Plus it is much easier studying technical subjects from a paper copy, where you can simultaneously hold one or more pages open to check referenced equations (and other things), write your own helpful notes and equations in margins and between lines, input corrections, and more.
Please also note that I have been considering writing a second volume on weak and strong interactions. But, since I am retired without a pension, I will be forced to do other things if the present book, due to electronic pirating, proves I will not be compensated for my time.
I thank you sincerely for paying for what I have offered you in this book.
Bob Klauber__________________________________________________________________________
Yes, I would like to support Klauber’s efforts to make learning physics easier by buying the book, and I certainly plan to do so when I am
prepared to actually work through the text, which may be about 5 years from now, the Devil willing, and the crick don't rise. For any serious study, I always recommend the hard copy text, and I only post links to the electronic versions to allow potential "physics students" to browse the material, where they may come to the conclusion that they have several if not many years of prerequisite mathematics to study before approaching this "user friendly" treatment of what still amounts to some very heady material.
I encourage the purchase of this text WHEN YOU ARE READY. Myself, even at the old age of soon to be 52, I have humbly embraced the reality that I must go over quite a bit of math for a few years (at least) before seriously approaching this text. In the meantime, it is cool to be able to browse through it to give us potential students an idea of where we need to focus our attention, as far as the math goes.
Talk about disillusionment! It is quite possible that, by the time some of us get around to purchasing this text, Mr. Bob might have "passed on," and yet, even in that case, a hard copy would be worth having for the serious autodidact. We'll keep our eyes peeled for this one. In the mean time, I would advise anyone remotely interested in "quantum theory" to be sure to be comfortable with basic "matrix theory," not to mention calculus-based physics, which requires a strong foundation in algebra, geometry, trigonometry, and, of course, what we call "Linear Algebra."
It may serve to bolster our egos when we equate matter and energy, and one may wonder if all the mathematical physics is even necessary. What would Schopenhauer do?
At this point, I can't even concern myself with wondering if Schopenhauer tinkered with differential equations and linear algebra. I know he had the capacity, but I suspect the tedium would aggravate him, as he wished to understand the riddle of existence in general. I have this feeling that Schopenhauer might find the technical (mathematical) details tedious drudgery.
To be honest, it can all become extremely depressing to consider how much time is required to build the mathematical foundation. An honest man must not allow himself to panic, and must guard against being discouraged by liars and egotistical academecians.
We must crawl before we can walk. It's a long road.
Before I would even think of studying quantum field theory or quantum mechanics, I would want to have a better grasp of basic VECTOR SPACES and linear transformations.
I wonder how many youth commit suicide over the thought of just how much there is to learn. Then I also wonder if so much knowledge can yield understanding.
Can one understand without such knowledge?
It appears that Schopenhauer may have understood on an intuitive level what had later been turned into a science via advanced mathematics.
Even if I never posses a small fraction of Schopenhauer's understanding, I would at least wish to spend the remainder of my life pecking away at the "baby math" so that I might have just enough knowledge to better understand a book like
Student Friendly Quantum Field Theory by Robert D. Klauber or even
Quantum Field Theory for the Gifted Amateur by Lancaster & Blundell - even if I am 68 years old studying it!

The important message I am trying to convey is that there is no shame in accepting that certain disciplines are beyond one's grasp, and that it is OK to return to high school and undergraduate mathematics for a good ten years. An article in a popular science magazine about Quantum Mechanics will not cut the mustard.
This is a concrete example of what it means to "unearth disillusionment." It's like saying, "I hate to burst your bubble, but ..."
On the other hand, I can offer some consolation to those who sincerely don't give a lick damn about such things: Understanding is not a requirement for this existence. The only requirements are birth and death. Why do I burden myself with the desire to understand "the math" ?
I have nothing better to do, and I do not pressure myself to actually understand anything at all, but only to peck away at gaining knowledge a little at a time, in baby steps, accepting the great likelihood that, in the end, a great deal of knowledge may lead to only a small degree of understanding. At least I will die with a totally deflated ego and welcome the sweet release of death's warm embrace!

------------------------------------------------------------------------------------------------------------------
FOOTNOTE : Simple example of mathematical representation of a qualitas occulta:
-------------------------------------------------------------------------------------------------------------------
from The World as Will and Representation, Volume 1, page 72
The theorem of Pythagoras teaches us a qualitas occulta of the right angled triangle; the stilted, and indeed subtle, proof of Euclid forsakes us at the why, and the accompanying simple figure, already known to us, gives at a glance far more insight into the matter, and firm inner conviction of that necessity, and of the dependence of that property on the right angle, than is given by his proof.---------------------------------------------------------------------------------------------------------------------------------
Now, the following image is not from Schopenhauer's work, but he is talking about intuitive knowing - directly through perception.
Rather than thinking a^2 + b^2 = c^2, we imagine
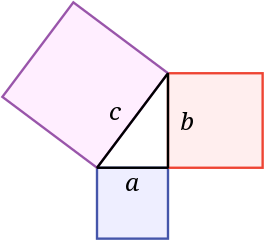
The sides are squared. You gain insight at a glance.
So what does Schopenhauer mean when he says "Pythagoras teaches us a qualitas occulta of the right-angled triangle"? Pythagoras teaches us the hidden quality of right-angled triangles? Pythagoras teaches us the ultimate cause or inner nature of right triangles?